本文章转载自3D视觉工坊

0、步态规划

四足机器人控制当中，步态是至关重要的一项。我们可以简单理解成四足机器人运动过程中各腿的状态，在这套设计方案中，我们对步态的规划主要分成两大主要部分，即接触状态和周期函数。而步态规划的目的，就是创建一个关于的足端接触状态的周期函数。

1、接触状态

四足机器人行进过程中，根据足端与地面是否发生接触，我们可以规定各条腿的两种接触状态，即接触（contact）与摆动（swing）

总控制器会根据步态规划给出的状态，移交至对应的控制器去处理，即摆动腿控制器（swing leg controll），接触腿控制器（contact leg control）。

对于这两种状态，可以简单地用一个布尔类型的值s来定义，即

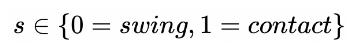
对于周期性的步态规划，我们可以用下标Φ来进行区分，可以写成：

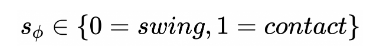
2、步态周期

四足机器人的运动归根到底都是周期运动，我们无须量化机器人运动的整个过程，因此如何量化定义一个完整的步态周期显得极为重要，在此我们使用基于时间的周期函数，定义一个基准相位值，公式如下：

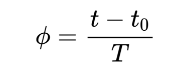
其中，

·  t：当前运行时间

·  t0：当前周期开始时间

·  T：一个步态周期

同样我们可以利用取余的方法来简化上述周期函数，两者并无实质的区别：

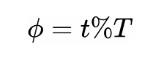
其中，

·  %为取余运算

·  T为当前运行时间

对于相同类型的周期信号，我们可以利用相位差来表征周期函数之间的差别，因此有了基准相位函数之后，我们就可以利用其来定义各条腿的相位，如下式：

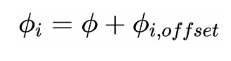
其中，Φi,offset为第条腿与基准相位的相位差。

3、周期函数效果演示

这里简单利用一个线性函数进行演示：

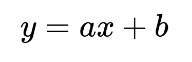
取a=1,b=1，其图像随时间变化如下：

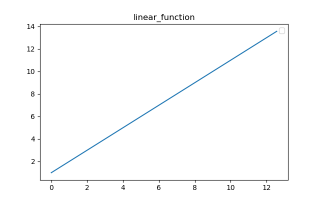
利用周期函数对时间进行调整，可以使其变成周期函数，设定周期为2s，时长为10s，其图像如下：

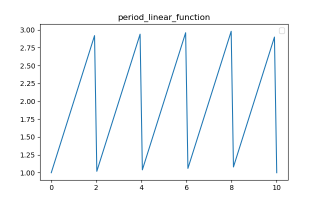
从图像可以看出，刚好为5个周期，一个周期为一个尖角。接下来，为更好的观察各曲线相位，我们设定该直线函数的3个周期，其相位差（offset）分别为[0,1,3,4]，图像如下：

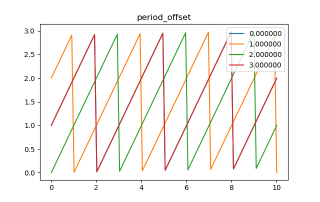
从上图可以看出，我们的“尖角”会根据相位差，向前或向后平移。此方法对所有函数均适用，以下为利用sin函数进行的测试效果：

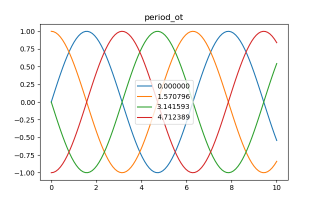
4、步态规划

因为我们的四足机器人足端，是在不停地与地面接触，悬空（摆动），所以这里说的步态规划，其实指的的一个连续（离散）时间上的接触序列。

我们以一条腿为例，本质上，可以看作是一个周期性的，用于生成各腿接触状态的阶跃函数。其输入值为时间，输出值为0或1，函数可以表示成如下：

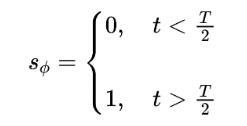
其中t=t%T为时间的周期函数，其图像如下所示：

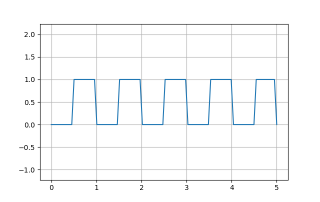
可以看出，步态规划器给出的是一段由0-1组成的接触序列。接下来加上相位关系。以tort步态为例，其相位为[0, 0.5, 0.5, 0]，步态规划随时间的图像如下所示：

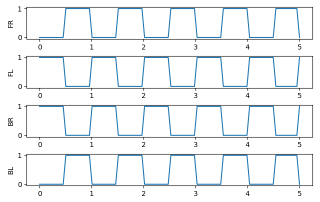
5、总结

综上，我们利用阶跃函数得到一串由0和1组成的序列，来表示四足机器人足端与地面的接触状态。根据不同的接触状态，再交由其他运动控制器进行控制，如接触状态，就由mpc模型计算出所需要的反作用力；而摆动状态，就交由摆动控制模块计算足端的摆动轨迹，最后根据需要的不同的行走姿态，确定个条腿之间的相位差，实现各腿的协同运动。